Estimated read time: 6-7 minutes
This archived news story is available only for your personal, non-commercial use. Information in the story may be outdated or superseded by additional information. Reading or replaying the story in its archived form does not constitute a republication of the story.
SALT LAKE CITY — What do the shape of snowflakes, the population of bee colonies, the growth patterns of trees, the spirals of a nautilus and the paintings of Leonardo Da Vinci have in common?
They all follow the rules and patterns of the Golden Ratio.
The Golden Ratio is also known as the Golden Number, the Golden Section and the Divine Proportion. Mathematicians call it φ or Phi (some pronounce it fee, others rhyme it with pie). It's about 1 to 1.618.
You can find the golden ratio all throughout Nature and art. Even human anatomy follows the Golden Ratio. Measure the distance from the tip of a person's head to the floor. Now measure the distance from that person's belly button to the floor and you get φ. The distance from shoulder to fingertip, as compared to the distance from elbow to fingertips, is φ. It also applies to a person's hip to floor as compared to knee to floor. Also the spacing between their finger joints, toe joints and spinal divisions.
But what is it really? How do you define it?
The Golden Ratio was first defined by the Greek mathematician Euclid of Alexandria, who is most famously known as the founder of geometry, around 300 B.C.
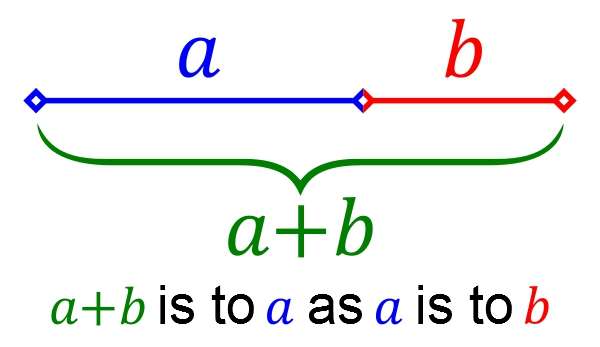
Euclid drew a line and divided it so that the ratio AB, as compared to AC, is proportionate to the ratio of AC to CB, thus dividing it into its extreme and mean ratios, expressed as 1:1.6180339887 ….
In other words, AB is 1.618 times larger than AC, and AC is 1.618 times larger than CB.
The Golden Ratio becomes even more intriguing when you add in the Fibonacci Sequence, which is a numeric progression in which each number is equal to the sum of the two preceding terms. Fibonacci’s full name was Leonardo de Pisa, but he was known as Fibonacci. He was an Italian mathematician who lived from 1170-1250 A.D. The Fibonnacci Sequence first appeared in his book "Liber Abaci" in 1202.
The first two numbers in the Fibonacci Sequence are zero and one. Add those two numbers together to get your next number, which will be one. Now, add those two numbers together to get your next number, which will be two. Now, add those two numbers together to get your next number, which will be three. You see the pattern.
The numbers in the Fibonacci Sequence are:
0 – 1 – 1 – 2 – 3 – 5 – 8 – 13 – 21 – 34, and on and on ad infinitum.
If you take any number on the Fibonacci Sequence and divide it by the number that precedes it, the sum/quotient will be amazingly close to φ. For instance, five divided by three equals 1.666. Thirteen divided by eight equals 1.625. But this equation doesn’t work at the very beginning of the sequence, as three divided by two equals 1.5.
On the face of it, the Golden Ratio just looks like a semi-interesting mathematical quirk that somehow aligns itself with another semi-interesting mathematical quirk. Taken on those strengths, it is really no more interesting than a puzzle in the New York Times or some bit of trivia that gets trotted out at a mathematician’s cocktail party. But what makes the Golden Ratio truly interesting is that it appears everywhere throughout nature. And often in some very unexpected places.
“The Golden Ratio’s attractiveness stems first and foremost from the fact that it has an almost uncanny way of popping up where it is least expected,” writes Mario Livio, author of "The Golden Ratio."
Pretty much any spiral you see occurring in nature follows the rules of the Golden Ratio. “Nature loves logarithmic spirals,” Livio writes. “From sunflowers, seashells and whirlpools to hurricanes and giant spiral galaxies, it seems that nature chose this marvelous shape as its favorite ‘ornament.’ ” The spiral logarithm also applies to the curve of a ram’s horns, the curve of elephant tusks, the shell of a snail. Many non-spiral forms of the Golden Ratio can also be found in nature. The spacing of branches on trees and snowflakes.
Most commonly you’ll find that the sections of an object in nature, that follows the rule of φ, grow smaller and smaller, with every subsequent segment smaller than its predecessor by a factor equal to φ. For instance, with snowflakes, the appearance of the first branch comparative to the source will occur at a random distance, but after that the appearance of the next branch will occur at a distance that is shorter by a factor equal to φ.

The spiraled shell of the nautilus is the exception to the rule. Its shell increases in size with each segment, each spiral growing larger by a factor of φ.
The ancient Greeks, having discovered and defined the Golden Ratio back in 300 B.C., now began seeing examples of it all around them in nature and suddenly saw order in an otherwise chaotic world. Since so many things seemed to follow this pattern, they were sure that they had just discovered God’s blueprint, and so they named the number the Divine Proportion.
Greek artists were quick to recognize the aesthetic properties of the Golden Ratio and incorporate it into their work, writes Livio. If God gives you blueprints, why not use them.
Architects, sculptors and painters began incorporating φ into their work. Mark Barr, an American mathematician, gave the Golden Ratio the name of "phi", with its corresponding symbol, naming it after the first Greek letter in the name of Phidias (490-430 B.C.), who incorporated the Golden Ratio into his sculptures.
But even though φ was discovered as early as 300 B.C., word of it didn’t become widespread until the Rennaisance, writes Livio.
If one studies the works of Albrecht Durer, Michelangelo, Leonardo Da Vinci (and numerous others), they will easily find what can only be intentional uses of φ in their artwork.
Antonio Stradivari, maker of the famous Stradivarius violins, used φ to calculate where to place the f-holes on his violins. Mozart is said to have used it to construct his sonatas, and Beethoven his Fifth Symphony. As strange and varied as the places you’ll the Golden Ratio in nature, you’ll find it in equally numerous and unexpected places throughout the art world.
“Biologists, artists, musicians, historians, architects, psychologists and even mystics have pondered and debated the basis of its ubiquity and appeal,” writes Livio. “In fact, it is probably fair to say that the Golden Ratio has inspired thinkers of all disciplines like no other number in the history of mathematics.”
If you have a science subject you'd like Steven Law to explore in a future article send him your idea at curious_things@hotmail.com.